|
ĐỀ THI TUYỂN SINH LỚP 10 NĂM HỌC 2012-2013
Môn thi: TOÁN (chuyên)
Ngày thi: 25/06/2012
Thời gian làm bài: 150 phút (không tính thời gian giao đề) Bài 1. (2,0 điểm) Giải hệ phương trình:
 Bài 2. (2,0 điểm)
Cho các số thực 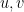 sao cho: sao cho: 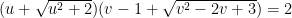 . Chứng minh rằng: . Chứng minh rằng:  Bài 3. (2,0 điểm)
Cho hai đường tròn 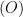 và và  cắt nhau tại A và B sao cho đoạn thẳng OO’ cắt đường thẳng AB. Đường thẳng cắt nhau tại A và B sao cho đoạn thẳng OO’ cắt đường thẳng AB. Đường thẳng 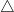 tiếp xúc với đường tròn tiếp xúc với đường tròn  tại C, tiếp xúc với tại C, tiếp xúc với  tại D và sao cho khoảng cách từ A đến tại D và sao cho khoảng cách từ A đến  lớn hơn khoảng cách từ B đến lớn hơn khoảng cách từ B đến  . Đường thẳng qua A song song với đường thẳng . Đường thẳng qua A song song với đường thẳng  cắt đường tròn cắt đường tròn  thêm điểm E và cắt đường tròn thêm điểm E và cắt đường tròn  thêm điểm F. Tia EC cắt tia FD tại G. Đường thẳng EF cắt các tia CB và DB tại H và K thêm điểm F. Tia EC cắt tia FD tại G. Đường thẳng EF cắt các tia CB và DB tại H và K
a) Chứng minh tứ giác  nội tiếp nội tiếp
b) Chứng minh tam giác 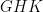 cân cân Bài 4. (2,0 điểm) a) Tìm các số nguyên dương lẻ 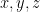 thỏa mãn đồng thời các điều kiện sau: thỏa mãn đồng thời các điều kiện sau:  và và 
b) Chứng minh tồn tại  số nguyên dương số nguyên dương  sao cho: sao cho:
 và và  Bài 5.(2,0 điểm) a) Chứng minh rằng diện tích của những tứ giác có các đỉnh nằm trong hoặc trên một đường tròn bán kính $R$ luôn nhỏ hơn hoặc bằng 
b) Cho x và y là các số thực dương thay đổi sao cho  . Tìm giá trị nhỏ nhất của . Tìm giá trị nhỏ nhất của  ———————————– Hết ———————————– Gợi ý giải một số bài (Tham khảo) Bài 1:
Hệ phương trình đã cho 
0= 2.(1)-(2) = (2a-b-4)(a+b+1) Bài 2:

Mà theo giả thiết: 
 (1) (1)
Tương tự :  (2) (2)
(1)-(2) vế theo vế: u+v=1
Ta có 
=  ( vì u+v=1 ) ( vì u+v=1 )
= 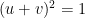 (vì u+v=1 ) (vì u+v=1 )
Vậy  (đpcm) (đpcm) Bài 3
a)  cân tại C,D Mà cân tại C,D Mà
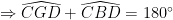
 Tứ giác BCGD nội tiếp Tứ giác BCGD nội tiếp
b) Ta có 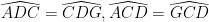
 (g_c_g) (g_c_g)
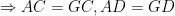
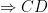 là đường trung trực của AG là đường trung trực của AG
 vuông góc EF (1) vuông góc EF (1)
AB cắt CD tại I
C/m được I là trung điểm CD
Theo Ta-let, ta có:

 A là trung điểm HK (2) A là trung điểm HK (2)
Từ (1) và (2)  tam giác AHK cân tam giác AHK cân Bài 4
a) 



x = 1;3 loại 
x = 5 thì 
y = 
Thế lại thấy y = 9  z = 45 (thỏa) z = 45 (thỏa)
x = 7 thì 
Giải tương tự được y = 7,z = 21
Vậy phương trình đã cho có 1 nghiệm nguyên dương lẻ thỏa mãn điều kiên x<y (x;y;z) = (5;9;45) Bài 5
a) Các tứ giác nằm trong đường tròn thì 2 cạnh chéo bé hơn 2 dây kéo dài đến đường tròn nên dễ dàng c/m được các tứ giác nằm trong đường tròn có diện tích bé hơn các tứ giác có các đỉnh nằm trên biên
Gọi tứ giác đó là ABCD, AK,CH vuông góc BD tại K,H
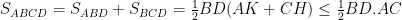
Mà 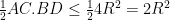
dấu bằng xảy ra khi ABCD là hình vuông
b)  mà mà 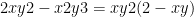 đặt a =xy suy ra đặt a =xy suy ra  mà mà 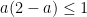 vâỵ minT = 4.dấu bằng xảy ra x = y = 1 vâỵ minT = 4.dấu bằng xảy ra x = y = 1
|